[107指考數甲，圓] 圓內兩線段互相垂直，求$\overline{CD}$長度

==問題== 

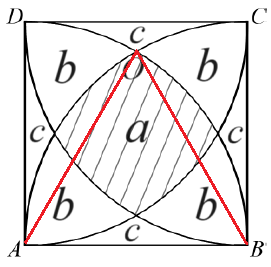
設$A$，$B$，$C$，$D$為圓上的相異四點。已知圓的半徑為$\frac{7}{2}$，$\overline{AB}=5$，兩線段$\overline{AC}$與$\overline{BD}$互相垂直，如圖所示（此為示意圖，非依實際比例）。則$\overline{CD}$的長度為何？（化成最簡根式）

[107，指考，數學甲]

==答案==

$2\sqrt{6}$

==解析==

設$\overline{AC}$與$\overline{BD}$的交點為$O$。然後再假設$\angle BAC = \theta$，於是$\overparen{BC}$之弧度為$2 \theta$。由於$\angle BDC$所對的弧也是$\overparen{BC}$，因此$\angle BDC = \theta$。

接著座標化，取$\overline{AC}$為$x$軸，$\overrightarrow{AC}$之方向為正向；取$\overline{BD}$為$y$軸，$\overrightarrow{BD}$之方向為正向。於是$O$點座標為$(0, 0)$。

再假設$\overline{CD} = x$，於是$\overline{OC} = x \sin \theta, \overline{OD} = x \cos \theta, \overline{OA} = 5 \cos \theta, \overline{OB} = 5 \sin \theta$，從而可得各點座標$A = (-5 \cos \theta, 0), B = (0, -5 \sin \theta), C = (x \sin \theta, 0), D = (0, x \cos \theta)$。

再設圓心為$K$，注意到$K$點的$x$座標與$\overline{AC}$中點的$x$座標相同，$y$座標與$\overline{BD}$中點的$y$座標相同，因此可得$K$點的座標為$\left( \frac{x \sin \theta - 5 \cos \theta}{2}, \frac{x \cos \theta - 5 \sin \theta}{2} \right)$。

由題目條件「圓的半徑為$\frac{7}{2}$」可知

$$\overline{KC} = \frac{7}{2},$$

$$\sqrt{ \left( \frac{x \sin \theta - 5 \cos \theta}{2} - x \sin \theta \right)^2 + \left( \frac{x \cos \theta - 5 \sin \theta}{2} - 0 \right)^2 } = \frac{7}{2},$$

等號兩邊左右同時平方，展開得

$$\frac{x^2 \sin^2 \theta + 10 x \sin \theta \cos \theta + 25 \cos^2 \theta + x^2 \cos^2 \theta - 10 x \sin \theta \cos \theta + 25 \sin^2 \theta}{4} = \frac{49}{4},$$

於是

$$\frac{(x^2 \sin^2 \theta + x^2 \cos^2 \theta) + (25 \cos^2 \theta + 25 \sin^2 \theta)}{4} = \frac{49}{4},$$

$$\frac{ x^2(\sin^2 \theta + \cos^2 \theta) + 25( \cos^2 \theta + \sin^2 \theta)}{4} = \frac{49}{4},$$

$$\frac{ x^2 \cdot 1 + 25 \cdot 1}{4} = \frac{49}{4},$$

$$x^2 + 25 = 49,$$

$$x^2 = 24,$$

$$x = \pm \sqrt{24} = \pm 2 \sqrt{6} \quad {\text{負不合}},$$

$$x = 2 \sqrt{6}.$$

因此所求$\overline{CD} = 2 \sqrt{6}$。

(解答終了)

正方形內扇形重疊區域面積問題

=題目=

如圖，ABCD 為正方形且邊長為1 公分，以各頂點為圓心，1 公分為半徑做$\frac{1}{4}$弧，試求斜線區域面積。

=答案=

$1+\frac{\pi}{3}-\sqrt{3}$

=詳解=

首先假設圖中各區域的面積分別為$a, b, c$，如下圖所示。

為了求出$c$的大小，我們可以連接$\overline{OA}$與$\overline{OB}$，然後考慮正三角形$OAB$與扇形$AOD$及扇形$BOC$，將這三個部分從整個正方形$ABCD$中扣掉後，就會得到一塊$c$的面積。如下圖所示。

因此

$$c = 1\times 1  - \frac{\sqrt{3}}{4}\cdot 1^2 - \pi \cdot 1^2 \cdot \frac{30}{360} - \pi \cdot 1^2 \cdot \frac{30}{360} = 1 - \frac{\sqrt{3}}{4} - \frac{\pi}{6}.$$

另外再看原圖中，可知整個正方形$ABCD$扣除$\frac{1}{4}$圓形$ABD$後，剩下的部分恰好是$2c+b$，也就有

$$2c+b = 1 - \pi \cdot 1^2 \cdot \frac{90}{360} = 1 - \frac{\pi}{4}.$$

因此

$$b = \left( 1 - \frac{\pi}{4} \right) - 2 \cdot \left( 1 - \frac{\sqrt{3}}{4} - \frac{\pi}{6} \right) = \frac{\pi}{12} + \frac{\sqrt{3}}{2} - 1.$$

於是

$$a = 1-4b-4c = 1-4 \cdot \left( \frac{\pi}{12} + \frac{\sqrt{3}}{2} - 1 \right) - 4\cdot \left( 1 - \frac{\sqrt{3}}{4} - \frac{\pi}{6} \right) = 1 + \frac{\pi}{3} - \sqrt{3}.$$

一道平面幾何的圓的問題

=題目=

如圖，已知兩平行線$L_1, L_2$與圓$\Gamma$交於$A, B, C, D$四點，連接$\overline{AD}, \overline{BC}$交於$P$點，且$\angle BPD = 45^\circ$。若直線$L_1$平分圓$\Gamma$的面積，則$\Delta ABP$的面積為$\Delta CDP$面積的幾倍？

=答案=

2倍

=詳解=

由於$L_1$平分$\Gamma$的面積，所以$\overline{AB}$為直徑。

由於$\angle ABC$與$\angle ADC$皆為圓周角，且都夾$\overparen{AC}$，所以$\angle ABC = \angle ADC$。又$\angle APB$與$\angle CPD$為對頂角，所以$\angle APB = \angle CPD$。因此$\Delta APB \sim \Delta CPD$。

過$P$做直線$L_3 \parallel \overline{AB}$，則由平行線內錯角相等可知$45^\circ = \angle ABP + \angle CDP (= 2\angle ABP = 2\angle CDP )$，即$\angle ABP = \frac{45^\circ}{2}$。

自$P$向$\overline{AB}$與$\overline{CD}$作垂線，設垂足分別為$M$與$N$。連接$\overline{AC}$，注意$\angle BCA = 90^{\circ}$。

假設圓$\Gamma$半徑長1。於是便可寫出$\overline{MB} = 1, \overline{PB} = \frac{1}{\cos 22.5^\circ}$。

再假設$\overline{PD}$是$\overline{PB}$的$k$倍。於是$\overline{PN} = k, \overline{PD} = \frac{k}{\cos 22.5^\circ}$。由於$\Delta PCD$是等腰三角形，其中$\overline{PC} = \overline{PD}$，所以$\overline{PC} = \frac{k}{\cos 22.5^\circ}$。

在$\Delta ABC$中，利用銳角三角函數的定義有

$$\frac{\frac{1}{\cos 22.5^\circ} + \frac{k}{\cos 22.5^\circ}}{2} = \cos 22.5^\circ.$$

整理得

$$\frac{k+1}{2 \cos 22.5^\circ} = \cos 22.5^\circ.$$

於是再利用半角公式得

$$k = 2 \cos^2 22.5^\circ - 1 = 2 \times \frac{1 + \cos 2 \times 22.5^\circ}{2} - 1 = \frac{1}{\sqrt{2}}.$$

這表示$\Delta PBA$與$\Delta PCD$邊長比為$1: \frac{1}{\sqrt{2}} = \sqrt{2}: 1$，從而面積比為$(\sqrt{2})^2: 1^2 = 2: 1$。

（解答終了）

一道帶參數的有理分式不等式

=題目=

已知對於任意實數$x$，不等式$\frac{2x^2 + 2kx + k}{4x^2 + 6x + 3} < 1$恆成立，試求實數$k$的範圍。

=答案=

$1 < k < 3$

=詳解=

遇到分式不等式，必須移項，使一邊變為0，然後再用分子分母同號或異號去求解。所以原本的不等式先變形為

$$\frac{2x^2 + 2kx + k}{4x^2 + 6x + 3} - 1 < 0.$$

接著化簡不等式左端的式子，

$$\frac{2x^2 + 2kx + k}{4x^2 + 6x + 3} - 1 = \frac{2x^2 + 2kx + k}{4x^2 + 6x + 3} - \frac{4x^2 + 6x + 3}{4x^2 + 6x + 3} = \frac{-2x^2 + (2k - 6)x + (k - 3)}{4x^2 + 6x + 3}.$$

從而不等式變為

$$\frac{-2x^2 + (2k - 6)x + (k - 3)}{4x^2 + 6x + 3} < 0.$$

分子除以分母為負，表示分子與分母必然異號，從而相乘的結果也必定為負。另外分母不可為0，所以我們轉而考慮以下的聯立不等式

$$\left\{ \begin{align*} &[-2x^2 + (2k - 6)x + (k - 3)](4x^2 + 6x + 3)<0 \\ &4x^2 + 6x + 3 \ne 0 \end{align*}.  \right.$$

分析分母$4x^2 + 6x + 3$，此為二次式，平方項係數為正，且判別式為$6^2 - 4 \cdot 4 \cdot 3 < 0$，所以恆正。

從而不等式$[-2x^2 + (2k - 6)x + (k - 3)](4x^2 + 6x + 3)<0$可化為

$$-2x^2 + (2k - 6)x + (k - 3) < 0.$$

（我們可以直接去掉不等式中的恆正因子而不用考慮是否需要變號）

為方便計算，將式子中的正負號變號，化為

$$2x^2 - (2k - 6)x - (k - 3) > 0.$$

這表示二次式$2x^2 - (2k - 6)x - (k - 3)$恆正。由於其中平方項係數為2，是正數，所以我們只需再確認判別式為負即可。

$${\text{判別式}}  = [-(2k-6)]^2 - 4 \cdot 2 \cdot [-(k-3)] < 0.$$

展開整理得

$$k^2 - 4k + 3 < 0.$$

然後再因式分解得

$$(k-3)(k-1) < 0.$$

便解出

$$1 < k < 3.$$

（解答終了）

[111學測數A，多項式與二次函數] 不可能是$y=g(x)$圖形頂點的$y$座標

 =題目=

設$f(x), g(x)$皆為實係數多項式，其中$g(x)$是首項係數為正的二次式。已知$\left( g(x) \right)^2$除以$f(x)$的餘式為$g(x)$，且$y=f(x)$的圖形與$x$軸無交點。試選出不可能是$y=g(x)$圖形頂點的$y$座標之選項。

(1) $\frac{\sqrt{2}}{2}$

(2) 1

(3) $\sqrt{2}$

(4) 2

(5) $\pi$

=答案=

(1)

=詳解=

由於二次式$y=g(x)$的圖形為拋物線，故假設其頂點為$(h, k)$，從而可將$g(x)$的式子寫為$y=a(x-h)^2+k$，其中正數$a$為$g(x)$的首項係數。

接著再假設$\left( g(x) \right)^2$除以$f(x)$的商式為$q(x)$，亦即有除法算式

$$\left( g(x) \right)^2 \div f(x) = q(x)...g(x).$$

將之改寫為乘法算式為

$$\left( g(x) \right)^2 = f(x) \cdot q(x) + g(x).$$

由於$g(x)$是二次式，所以$\left( g(x) \right)^2$為四次式。另外因為除法餘式的次數必小於除式的次數，從而除式$f(x)$的次數為三次或四次。

但如果$f(x)$的次數為三次，那麼其圖形$y=f(x)$必會與$x$軸有交點，和題目條件矛盾。所以$f(x)$的次數必為四次。

再看回除法算式$\left( g(x) \right)^2 = f(x) \cdot q(x) + g(x)$，既然$\left( g(x) \right)^2$為四次、$f(x)$為四次，那麼商式$q(x)$一定是（非零）常數，設為$A$。重新改寫乘法算式得

$$\left( g(x) \right)^2 = f(x) \cdot A + g(x).$$

然後移項得

$$\begin{align*}f(x) \cdot A &= \left( g(x) \right)^2 - g(x) \\ &= g(x)[g(x) - 1] \\ &= [a(x-h)^2 + k][a(x-h)^2 + (k-1)]. \end{align*}$$

因此

$$f(x) = \frac{1}{A}[a(x-h)^2 + k] [a(x - h)^2 + (k-1)].$$

由於$y=f(x)$的圖形與$x$軸無交點，因此對於任意實數$x$而言，$a(x-h)^2 + k$與$a(x - h)^2 + (k-1)$都不等於0。又已知平方項係數為正之二次函數圖形必開口向上，從而$a(x-h)^2 + k$與$a(x - h)^2 + (k-1)$都恆正。

由$a(x - h)^2 + k$恆正可知$k>0$。

由$a(x - h)^2 + (k-1)$恆正可知$k-1>0$，即$k>1$。

綜上所述得$k>1$。所以選(1)、(2)。

（解答終了）