經典推導法
首先是我們的老朋友,$30^{\circ}-60^{\circ}-90^{\circ}$三角形,姑且就直接設定邊長是$1, \sqrt{3}$與$2$,如下圖所示:
接著我們延伸底邊$\sqrt{3}$,向右伸長$2$,然後再與原來三角形的頂點連接,如下圖所示:注意這樣做的結果就是在本來的三角形的右側生出一個等腰三角形,而且兩底角都是$15^{\circ}$!
我們就獲得一個$15^{\circ}-75^{\circ}-90^{\circ}$的直角三角形。
接著開始來計算斜邊:
$$\sqrt{1^2 + (2+\sqrt{3})^2} = \sqrt{1 + 4 + 4\sqrt{3} + 3} = \sqrt{8 + 2\sqrt{12}} = \sqrt{(\sqrt{6} + \sqrt{2})^2} = \sqrt{6} + \sqrt{2}.$$
於是就可以求出
$$\sin 15^{\circ} = \frac{1}{\sqrt{6} + \sqrt{2}} = \frac{1 \cdot (\sqrt{6} - \sqrt{2})}{(\sqrt{6} + \sqrt{2})(\sqrt{6} - \sqrt{2})} = \frac{\sqrt{6} - \sqrt{2}}{4},$$
$$\cos 15^{\circ} = \frac{2 + \sqrt{3}}{\sqrt{6} + \sqrt{2}} = \frac{(2 + \sqrt{3}) \cdot (\sqrt{6} - \sqrt{2})}{(\sqrt{6} + \sqrt{2})(\sqrt{6} - \sqrt{2})} = \frac{\sqrt{6} + \sqrt{2}}{4}.$$
然後利用$\sin (90^\circ - \theta) = \cos \theta$可以再求出
$$\sin 75^{\circ} = \sin (90^\circ - 15^\circ) = \cos 15^\circ = \frac{\sqrt{6} + \sqrt{2}}{4},$$
$$\cos 75^{\circ} = \cos (90^\circ - 15^\circ) = \sin 15^\circ = \frac{\sqrt{6} - \sqrt{2}}{4}.$$
然後我們可以開始計算$\tan$,利用$\tan \theta = \frac{\sin \theta}{\cos \theta}$,得
$$\tan 15^\circ = \frac{\sin 15^\circ}{\cos 15^\circ} = \frac{\frac{\sqrt{6} - \sqrt{2}}{4}}{\frac{\sqrt{6} + \sqrt{2}}{4}} = \frac{\sqrt{6} - \sqrt{2}}{\sqrt{6} + \sqrt{2}} = \frac{(\sqrt{6} - \sqrt{2})^2}{(\sqrt{6} + \sqrt{2})(\sqrt{6} - \sqrt{2})} = \frac{8 - 4\sqrt{3}}{4} = 2 - \sqrt{3},$$
$$\tan 75^\circ = \frac{\sin 75^\circ}{\cos 75^\circ} = \frac{\cos 15^\circ}{\sin 15^\circ} = \frac{1}{\frac{\sin 15^\circ}{\cos 15^\circ}} = \frac{1}{\tan 15^\circ} = \frac{1}{2 - \sqrt{3}} = \frac{1\cdot (2 + \sqrt{3})}{(2 - \sqrt{3})(2 + \sqrt{3})} = 2 + \sqrt{3}.$$
整理
$$\begin{array}{ccc} & 15^\circ & 75^\circ \\ \sin & \frac{\sqrt{6} - \sqrt{2}}{4} & \frac{\sqrt{6} + \sqrt{2}}{4} \\ \cos & \frac{\sqrt{6} + \sqrt{2}}{4} & \frac{\sqrt{6} - \sqrt{2}}{4} \\ \tan & 2 - \sqrt{3} & 2 + \sqrt{3} \end{array}$$
正方形內嵌正三角形推導法
由於$\overline{AB} = \overline{AD}, \overline{AE} = \overline{AF}, \angle ABE = \angle ADF = 90^\circ$,所以$\triangle ABE \cong \triangle ADF$(SAS)。從而$\angle BAE = \angle FAD = 15^\circ$。
為方便起見,我們取$\overline{AE} = 1$,於是$\overline{AB} = \cos 15^\circ, \overline{BE} = \sin 15^\circ, \overline{EC} = \frac{\sqrt{2}}{2}, \overline{FC} = \frac{\sqrt{2}}{2}, \overline{FD} = \sin 15^\circ, \overline{AD} = \cos 15^\circ.$
比較$\overline{AB}$與$\overline{DC}$,得等式
$$\cos 15^\circ = \sin 15^\circ + \frac{\sqrt{2}}{2}.$$
左右兩邊同時平方,化簡得
$$\sin 15^\circ \cos 15^\circ = \frac{1}{4}.$$
從而有
$$\cos 15^\circ + \sin 15^\circ = \sqrt{(\cos 15^\circ + \sin 15^\circ)^2} = \sqrt{1 + 2\cdot \frac{1}{4}} = \frac{\sqrt{6}}{2}.$$
因此由$\left\{ \begin{array}{l} \cos 15^\circ - \sin 15^\circ = \frac{\sqrt{2}}{2} \\ \cos 15^\circ + \sin 15^\circ = \frac{\sqrt{6}}{2} \end{array} \right.$解得
$$\sin 15^\circ = \frac{\sqrt{6} - \sqrt{2}}{4}, \cos 15^\circ = \frac{\sqrt{6} + \sqrt{2}}{4}.$$
其他相關角度的三角函數值
- 點$(x, y)$對$x$軸對稱的結果為$(x, -y)$,對$y$軸對稱的結果為$(-x, y)$。
- 比較少用的是,過原點而斜率為$m$的直線,無論是對$x$軸對稱還是對$y$軸對稱,結果都是過原點而斜率為$-m$的直線。
- 最為少用的是,過原點而斜率為$m$的直線,若對直線$y = x$對稱,則結果是過原點而斜率為$\frac{1}{m}$的直線。(事實上,這結果就是反函數微商公式$\frac{dy}{dx} = \frac{1}{\frac{dx}{dy}}$!)
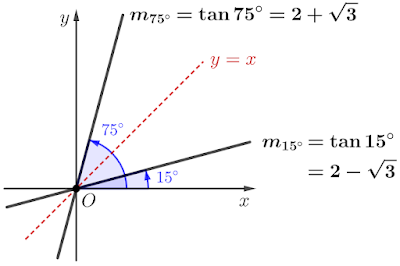
我們的出發點就是下面這個三角形:
以及兩條直線的斜率:$105^\circ$的三角函數值
下面其他角度列出計算過程,請讀者自己想出我是怎樣進行對稱。
$165^\circ$的三角函數值
$$\sin 165^\circ = \sin 15^\circ = \frac{\sqrt{6} - \sqrt{2}}{4},$$
$$\cos 165^\circ = -\cos 15^\circ = - \frac{\sqrt{6} + \sqrt{2}}{4},$$
$$\tan 165^\circ = - \tan 15^\circ = -(2 - \sqrt{3}).$$
$195^\circ$的三角函數值
$$\sin 195^\circ = - \sin 165^\circ = -\frac{\sqrt{6} - \sqrt{2}}{4},$$
$$\cos 195^\circ = \cos 165^\circ = - \frac{\sqrt{6} + \sqrt{2}}{4},$$
$$\tan 195^\circ = - \tan 165^\circ = -[-(2 - \sqrt{3})] = 2 - \sqrt{3}.$$
$255^\circ$的三角函數值
$$\sin 255^\circ = - \sin 105^\circ = -\frac{\sqrt{6} + \sqrt{2}}{4},$$
$$\cos 255^\circ = \cos 105^\circ = - \frac{\sqrt{6} - \sqrt{2}}{4},$$
$$\tan 255^\circ = - \tan 105^\circ = -[-(2 + \sqrt{3})] = 2 + \sqrt{3}.$$
$285^\circ$的三角函數值
$$\sin 285^\circ = \sin 255^\circ = -\frac{\sqrt{6} + \sqrt{2}}{4},$$
$$\cos 285^\circ = \cos 75^\circ = \frac{\sqrt{6} - \sqrt{2}}{4},$$
$$\tan 285^\circ = - \tan 255^\circ = -\tan 75^\circ = -(2 + \sqrt{3}).$$
$345^\circ$的三角函數值
$$\sin 345^\circ = \sin (-15^\circ) = -\sin 15^\circ = -\frac{\sqrt{6} - \sqrt{2}}{4},$$
$$\cos 345^\circ = \cos (-15^\circ) = \cos 15^\circ = \frac{\sqrt{6} + \sqrt{2}}{4},$$
$$\tan 345^\circ = -\tan 15^\circ = -(2 - \sqrt{3}).$$










沒有留言:
張貼留言