正方形內扇形重疊區域面積問題

=題目=

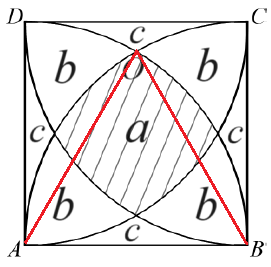
如圖，ABCD 為正方形且邊長為1 公分，以各頂點為圓心，1 公分為半徑做$\frac{1}{4}$弧，試求斜線區域面積。

=答案=

$1+\frac{\pi}{3}-\sqrt{3}$

=詳解=

首先假設圖中各區域的面積分別為$a, b, c$，如下圖所示。

為了求出$c$的大小，我們可以連接$\overline{OA}$與$\overline{OB}$，然後考慮正三角形$OAB$與扇形$AOD$及扇形$BOC$，將這三個部分從整個正方形$ABCD$中扣掉後，就會得到一塊$c$的面積。如下圖所示。

因此

$$c = 1\times 1  - \frac{\sqrt{3}}{4}\cdot 1^2 - \pi \cdot 1^2 \cdot \frac{30}{360} - \pi \cdot 1^2 \cdot \frac{30}{360} = 1 - \frac{\sqrt{3}}{4} - \frac{\pi}{6}.$$

另外再看原圖中，可知整個正方形$ABCD$扣除$\frac{1}{4}$圓形$ABD$後，剩下的部分恰好是$2c+b$，也就有

$$2c+b = 1 - \pi \cdot 1^2 \cdot \frac{90}{360} = 1 - \frac{\pi}{4}.$$

因此

$$b = \left( 1 - \frac{\pi}{4} \right) - 2 \cdot \left( 1 - \frac{\sqrt{3}}{4} - \frac{\pi}{6} \right) = \frac{\pi}{12} + \frac{\sqrt{3}}{2} - 1.$$

於是

$$a = 1-4b-4c = 1-4 \cdot \left( \frac{\pi}{12} + \frac{\sqrt{3}}{2} - 1 \right) - 4\cdot \left( 1 - \frac{\sqrt{3}}{4} - \frac{\pi}{6} \right) = 1 + \frac{\pi}{3} - \sqrt{3}.$$